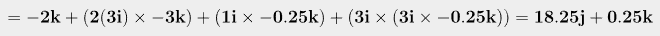3차원 강체의 운동학
고정 좌표계와 이동 좌표계에서 관찰된 벡터의 시간 미분. r 벡터의 크기성분과 방향성분을 각각 chain rule 로 미분하였을 때, 크기성분의 미분 측은 "회전 좌표계" 에서의 속도 성분과 같다(회전좌표계에선 방향이 항상 일정함.)
그리고 방향성분의 미분측은 "고정 좌표계에서 본 회전 좌표계의 각속도" 와 거리벡터의 외적 곱과 같다.



EX) -1k rad/s 만큼 회전하는 큰 원판 위에 작은 원판이 축의 관계가 수직하게 돌고있음. 큰 원판과 함께 돌아가는 회전 좌표계 기준, 작은 원판은 3j rad/s 의 각속도를 가지며 회전함. 작은 원판은 O점과 1m 떨어진 궤도를 따라 돌며, 반지름이 0.25m 일때 A 의 거리 벡터가 (1j + 0.25k) 인 순간 속도와 가속도를 구하라.
1. 오일러 정리에 의해 미소 회전 요소는 단순 벡터 덧셈 연산이 가능함.

2. 각 가속도를 구하기 위해 "큰 원판과 함께 돌아가는 회전 좌표계" 는 고정좌표계 기준 각 속도가 -1k rad/s 이다.

3. w_big 의 각 가속도는 직관적으로 0 임을 알 수 있다. 곧 (2) 의 각 가속도가 전체 각 가속도 이다.
4. 아래의 수식에 구한 값을 대입하여 거리벡터가 1j + 0.25k 인 순간 가속도와 속도를 구한다.

EX) 한 순간 Z축으로 회전하는 원판은 O점 기준 각속도 5k 와 각가속도 2k 로 각운동을 한다. 또한 O점과 A점은 사이에 거리벡터 2i 만큼 떨어져 있으며 A점 역시 원판과 같이 움직인다. 또한 A점은 3i 만큼의 각속도, 1i 만큼의 각가속도 운동을 하여 C점을 돌린다. C점은 A점과 한 순간 -0.25k 만큼 떨어져 있으며 -3k 만큼의 속도와 -2k 만큼의 가속도로 운동한다. 이때 C점의 속도와 가속도를 구해보자.
0. 우선 rel 은 회전좌표계를 뜻하며, int 는 고정 좌표계를 뜻함. 위 문제에선 O점 회전을 배제하는 relO 와 A점 회전까지를 배제하는 relA가 있음.
1. 우선 이는 "한 순간" 에 해당함. 가장 많은 회전요소를 가진 부분부터 회전 좌표계를 이용하여 점차적으로 해결해 나가야 한다. C의 경우 A점과 -3k의 속도와 -2k 의 가속도를 가진다고 볼 수 있음. 이는 다르게 표현하여 아래와 같다.

여기서 relA 는 A 점의 각운동과 같은 좌표계 상의 운동을 뜻하며, 두가지의 회전운동이 배제된 값이라는 것을 직관적으로 알 수 있다.
2. c 를 relO 좌표계를 이용해 표현해보자. 이는 우선 A점이 3i만큼의 각속도와 1i 만큼의 가속도를 가지고 있음을 나타내며, 이를 함께 고려하여야 한다. 여기서 relO 는 relA에 영향을 미치며, relA 는 단독으로 움직인다.

즉 초기 거리 r_c/a 를 이용하여 회전좌표계 O 상에서의 C점의 속도는 다음과 같다. (원점이 A라 가정)

또한 relO 상 C점의 가속도는 속도의 미분이므로 아래와같이 두 항이 전개되며, 회전좌표계 내의 벡터라 할 지라도 이를 시간미분할 때는 고정좌표계(여기서는 relO) 의 시간미분에 따른 방향정보가 포함됨. 즉 코리올리 가속도를 포함한 공식을 사용. (회전 좌표계, 여기서는 원점이 A )