강체의 운동학 (1)

우선의 해석은 강체가 고정된 기준 좌표에 대해 대칭이고, 주어지는 힘 또한 평면상에서 작용한다고 가정함. 물체의 운동은 기준좌표 내에서 나타낼 수 있으므로, 물체에 작용하는 모든 힘은 평면 위에 투사할 수 있음.

 

G = 질량중심

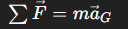
점 P를 통과하고, 운동평면에 수직인 축(z축) 에 대한 외력계가 모먼트에 미치는 영향을 살펴보자. 임의의 P점과 거리벡터 r 만큼 떨어져있는 i 질점에 대한 단순 표현은 아래와 같다.

 

 

이는 임의의 P점에 대한 i점이 일으키는 모먼트와 같음.

 

이에 mr 를 묶고, 가속를 n_t 좌표계 연산을 통해 아래와 같이 표현할 수 있다.

 

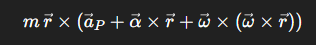
또한 거리성분을 (x,y) 로, 가속도 성분을 (aPx,aPy) 로 나눈 후 전개 시 아래와 같은 식이 나옴.

 

m을 dm과 적분표현으로 놓으면 아래와 같음

 

각 더하기 빼기로 연결된 항을 적분으로 나눈 다음 보면, 3 항이 각각 아래와 같이 표현 가능함.

 

여기서 x_G 나 y_G 는 P 점에서 G 점 까지의 거리임.